The maths shows that loss of immunity due to infections balances out infections reduced through population-wide interventions.
Interventions designed to limit the spread of covid have been rolled back around the world. In New Zealand, the government removed all remaining public health measures last week.
But although the emergency is over and the disease is rapidly becoming endemic, the risk of new variants remains. Covid is still causing a significant health burden.
“Public health officials have advised risk from COVID-19 is now considered low compared to other stages of the pandemic and it’s safe to remove the final requirements.”
— Sacha Dylan (@SachaDylan) August 14, 2023
Low for who?https://t.co/TrCmDmtzry
Is there more we could be doing to prevent infections?
We lack quality evidence about how effective different interventions are. But simple maths shows that, in the long term, the prevalence of a highly infectious endemic virus like SARS-CoV-2 is quite difficult to budge.
The basic reproduction number
Back in 2020, we heard a lot about the basic reproduction number or R0. This is the average number of people someone infects when the whole population is susceptible to the disease. With a susceptible population, if R0 is above 1 the disease spreads exponentially.
This situation prompted governments around the world to implement intensive response measures, including lockdowns, to prevent health systems from becoming completely overwhelmed.
The situation in 2023 is vastly different. Almost everyone has some form of immunity, acquired either from vaccination, previous infection, or both. However, people will eventually become susceptible again because of waning immunity and new variants.
This in turn means the virus won’t disappear altogether. Instead, the prevalence of infection will eventually reach what mathematicians call an endemic equilibrium. This is a state of balance: the loss of immunity due to its waning (and the cycle of births and deaths) is balanced by new immunity due to infections and vaccinations.
We don’t expect infection rates to be perfectly steady. Prevalence will rise and fall, influenced by seasons, school holidays and new subvariants, but it will always be pulled back towards the equilibrium level.
Controlling the disease
Unlike measles or polio, it’s impossible to eliminate covid with the tools currently available. But that doesn’t mean we can’t reduce its impacts. Effective control measures should reduce the number of contacts infectious people have, or the risk of infection per contact. And this should lower the level of the endemic equilibrium, meaning there are fewer infections.
That’s certainly true, but how much effect do control measures realistically have for a virus like SARS-CoV-2?
R0 for the Omicron variant has been estimated between 6 and 10. But the effective reproduction number – the average number of people someone infects at the present time – is much closer to 1. In New Zealand, this number has hovered between 0.8 and 1.2 for the past year.
This tells us something about the amount of immunity in the population. If an average person would infect six people in a fully susceptible population, but only infects one person in reality, that means five out of six people must be immune. If R0=10, then nine out of ten people must be immune, and so on.
The maths of immunity
People may have acquired immunity through vaccination, but the protection vaccines provide against infection with current Omicron variants is relatively low and short-lived.
The majority of immunity comes from previous infections, including infections in vaccinated people. This is called “hybrid immunity” and it provides better protection than infection or vaccination alone. (This doesn’t mean that getting infected to get immunity should ever be a goal, but it is an important side effect).
A consequence of this is that the fraction of the population that is immune at a given point in time is proportional to the number of infections per year. It turns out this allows us to estimate the benefit of interventions.
For example, suppose R0=6 and a control measure, such as isolation of all confirmed cases, reduces infectious contacts by 20%. That’s equivalent to reducing R0 to 4.8, which means the immune fraction is reduced from 83% of the population to 79%. That’s only a 5% relative reduction in the number of yearly infections, even though the transmission rate was reduced by 20%.
If R0=10, the maths is even more dismal: the same control measure only gives a 3% reduction in infections.
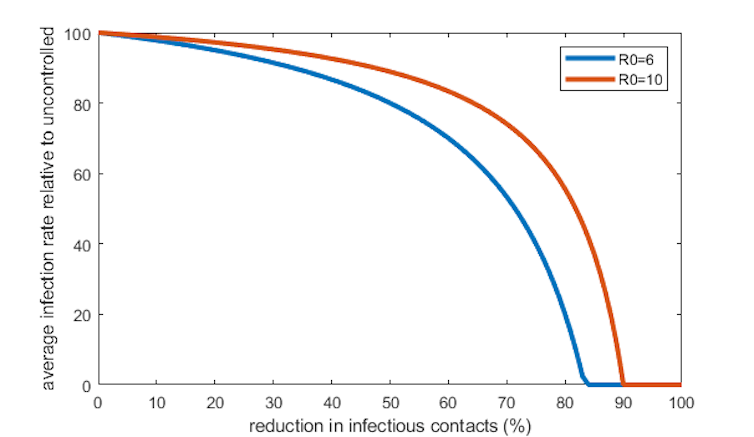
What’s the reason for this surprising finding? To begin with, the intervention reduces the number of infections, which is good. But an unfortunate side effect is that fewer people become immune, which means infections start to increase again.
Things eventually balance out at a lower level than without the intervention, but most of the benefit is sucked up by compensating for the lost immunity in the population.
For pathogens that are much less infectious than SARS-CoV-2, the opposite can be true. If R0=1.2, then a 20% reduction in infectious contacts would be enough to set the disease on a trajectory towards total elimination.
Targeted protection
The arguments above come from a mathematical model that captures the processes behind disease transmission in a simple way. Reality is more complicated. The susceptible-immune binary is a simplification because immunity is not black and white but shades of grey.
And populations are highly varied, not homogeneous. Infections will be more frequent in groups with high contact rates, which typically means younger people. Mathematically, that means infection rates will be harder to budge in younger groups and relatively easier to bring down in older groups.
Interventions targeted towards vulnerable groups are likely to be more effective than blanket measures. Importantly, although reducing infection rates in the long term is difficult, vaccines provide direct protection for those who take them and continue to be highly effective at preventing severe disease.
None of this is an argument that we shouldn’t try to reduce the prevalence of endemic diseases like covid. But it does mean we can’t assume that a reduction in the number of infectious contacts will translate to an equivalent reduction in infection rates.
Decreasing the number of SARS-CoV-2 infections would be highly beneficial. It would reduce the acute health burden, the incidence of long covid, and the level of risk for vulnerable groups.
But it’s not a goal we can afford to pursue at any cost. There is a range of healthcare needs competing for limited resources, so any measures need to be cost effective. And that means being realistic about the size of the benefits they’re likely to deliver.
Michael Plank is a professor in Applied Mathematics at University of Canterbury. Freya Shearer is a research fellow in Epidemic Decision Support at The University of Melbourne. James McCaw is a professor in Mathematical Biology at The University of Melbourne. James Wood is a professor of epidemiological modelling of infectious diseases at UNSW Sydney.
This article is republished from The Conversation under a Creative Commons licence. Read the original article.


